2017.04.03

iPhoneカメラ＆画像認識で球速計測（いわゆるスピードガン）が実現できるか？

こんにちは。F.S.です。
今回はお遊びネタで、iPhoneを使ったスピードレーダーの開発にトライしてみました。

※「スピードガン」はアメリカのディケイター・エレクトロニクス社の登録商標であり、一般的にはスピードレーダーと言うようです。

SCOUTEE のような本来の原理を用いた真面目なものではなく、またTangoのような深度センサーを使ったものではなく、一般化しているスマホを使って手軽に実現できそうなものを考えました。その分、高い測定精度は求めていません。
アプリストアには単純に投球距離÷時間で速度を出すものがありますが、距離を測って設定したりせずに手軽に測定できるものを考えました。

結論

実現度：△×

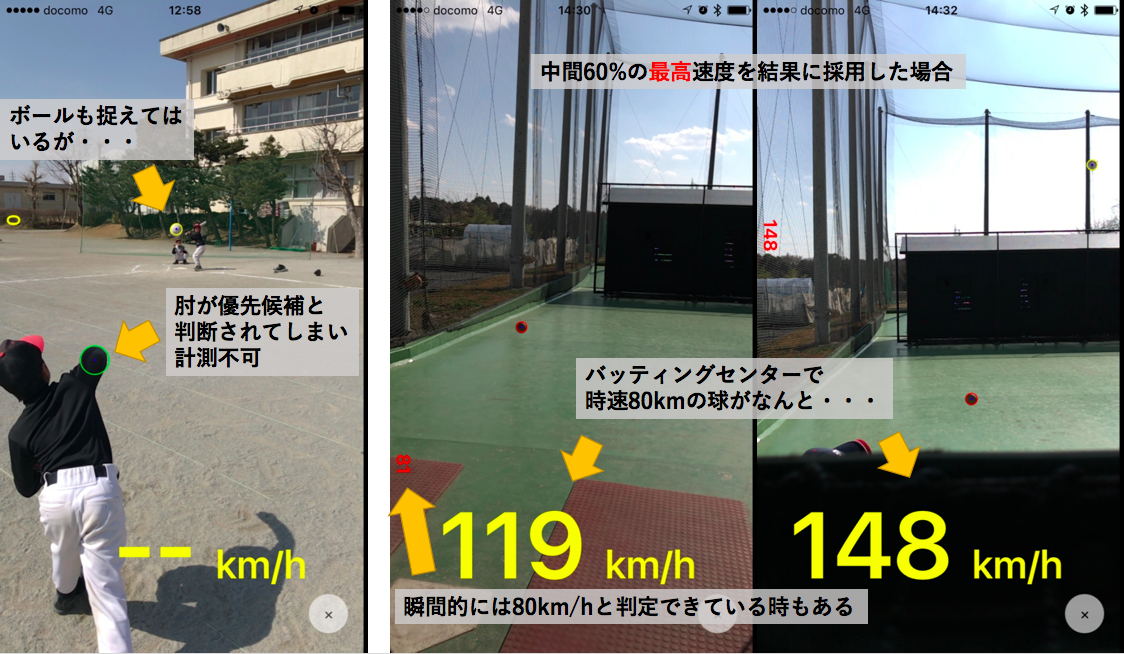
上の例のようにキレイにボールが検出できればそれなりの結果が出ます。
ただし、撮影場所によっては高頻度でボール以外の物体を優先的に検出してしまい、撮影のコツも必要で実用は難しいという結論です。。

これで終わるのも寂しいので、、何かの参考になることを願って今回考案した仕組みを記録しておきます。

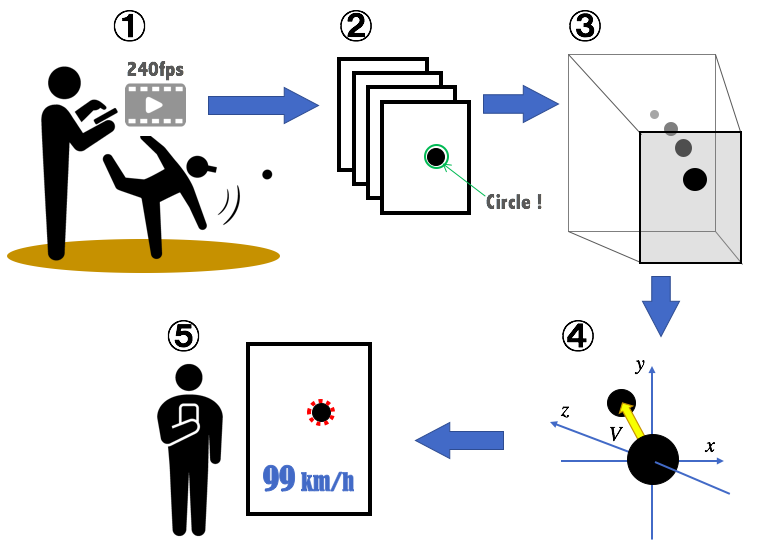
考案した仕組み

投球を240fpsのスローモーションで撮影
1フレームずつ画像認識で球体検出
画像における球体の2次元座標を3次元実空間に変換
3次元実空間におけるボール位置の変化量から速度を算出
結果を表示

iPhone6から240fpsのスローモーション撮影が可能になったということで、スローモーション撮影画像から球体の認識が出来るのではないかと考えました。240fpsだと時速100km（少年野球なら十分）であればフレーム間で11.5cm進むことになります。この程度であれば接写でない限りはっきりとした球体が捉えられるのではないかと予想しました。

1. 投球をスローモーション撮影

ボールの直径は7cm前後です。投球を撮影するため、ボールまである程度の距離があると想定されます。その際、画像に映るボールの変化量を求めるにはそれなりの解像度が必要になると考え、240fpsで撮影可能な最高解像度である1280×720を選択しています。

カメラ周りの処理は冗長的なのでコードは記載しませんが、実装のポイントは下記の通りです。

キャプチャセッションの sessionPreset に AVCaptureSessionPreset1280x720 を指定する
maxFrameRate = 240 のキャプチャデバイスを使用し、デバイスの activeVideoMin(Max)FrameDuration に 1/240 を指定する
アウトプットに AVCaptureVideoDataOutput を使用し、デリゲートを実装してキャプチャバッファが送られてくるたびに画像処理をする（240fpsのフレームレートから遅れたバッファは捨てる）

ARのようにリアルタイムで結果を投影するのは計算が追いつかないだろうという予想で、短時間撮影した後に解析する手法をとりました。
最終的に0.4秒間撮影することにしたのですが、この場合は結果出力まで800MB超のメモリを使用してしまいます。処理済みのフレーム画像は捨てていけば省メモリなのですが、結果表示に使いたいためメモリに残しています。

2. 画像認識で球体検出

2次元画像上では球体＝円と考えられるので、検出にハフ変換が使えます。ハフ変換は画像から直線や円を検出する手法です。

ハフ変換 – Wikipedia
https://ja.wikipedia.org/wiki/ハフ変換
Hough変換による画像からの直線や円の検出 – Codezine
https://codezine.jp/article/detail/153

ハフ変換はOpenCVに実装されてますので、これを使うことにしました。CocoaPodsでOpenCVをインストールして使用します。
なお、OpenCVに実装されているのは２段階ハフ変換で、エッジ検出処理を含んだものになっています。

cv::HoughCircles – opencv 2.2 documentation
http://opencv.jp/opencv-2svn/cpp/feature_detection.html#cv-houghcircles

ハフ変換により検出した円の中心座標と半径を得る実装例（Objective-C）はこちらのようになります。

+(NSArray *)detect:(UIImage *)image
{
    // iOSのUIImageをOpenCVのMat形式に変換し、グレースケールの画像データを作成する
    cv::Mat gray;
    UIImageToMat(image, gray);
    cv::cvtColor(gray, gray, cv::COLOR_BGR2GRAY);

    // Gaussianフィルターでぼかしを入れ、ノイズを減らす
    GaussianBlur( gray, gray, cv::Size(5, 5), 2, 2 );

    std::vector<cv::Vec3f> circles;

    HoughCircles(
        gray, 
        circles, 
        CV_HOUGH_GRADIENT, 
        1,     // 画像分解能に対する投票分解能の比率の逆数
        60,    // 検出される円の中心同士の最小距離
        200,   // Canny() エッジ検出器に渡される閾値
        24,    // 円の中心を検出する際の投票数の閾値
        10,    // 円の半径の最小値
        30     // 円の半径の最大値
    );
    
    NSMutableArray *circlesArray = [NSMutableArray array];
    for( size_t i = 0; i < circles.size(); i++ )
    {
        circlesArray[i] = @[
            [NSNumber numberWithFloat:circles[i][0]], // 中心の x 座標
            [NSNumber numberWithFloat:circles[i][1]], // 中心の y 座標
            [NSNumber numberWithFloat:circles[i][2]]  // 半径
        ];
    }

    return circlesArray;
}

画像の前処理や検出パラメータは試行錯誤が必要です。
ハフ変換では投票により円の候補が幾つか検出されますが、期待通りに円を検出するのはなかなか難しいです。一番投票を集めた円が、測定対象のボールになるとは限りません。

試行錯誤の結果、今回の用途では 1.5 〜 4.0m 離れた位置で撮影されるボールの検出が比較的精度が良かったため、半径10 〜 30pixの円を対象に検出するようにしています。
また、前処理に二値化やGammaフィルターを試してみましたが、ボールの陰影によって実際より小さな半径で検出されてしまう場合があるのでやめました。

どの円を測定対象のボールとみなすか？

パラメータを調整することで対象物を検出しやすくはできますが、それでも幾つかの候補が検出されてしまいます。
今回やろうとしているのは、連続したフレームからボールをトラッキングして速度を出すことです。対象は移動物体のため、フレーム間で xy 座標の変化が一定量以内でかつ変化量があるものを投球ボールと判断しています。

3. 画像における球体の2次元座標を3次元実空間に変換

一般的に次元の低いものから高い情報へ変換することは不可能で、次元が低い分は変動パラメータになってしまいます。
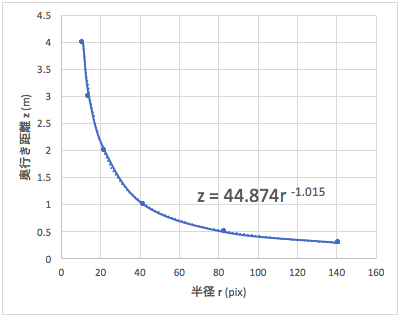
カメラの焦点距離とか射影変換とか調べるほどにハマってしまいましたが、今回は撮影対象のボールのサイズは決まっているため、実測値から奥行きの距離に変換することができます。実測値は、カメラからの距離と撮影されたボール半径のピクセル数を数点サンプリングし、近似式をとったものを使用します。近似式は指数関数が最適と判断しました。

これにより半径(r)を奥行き距離(z)に変換します。
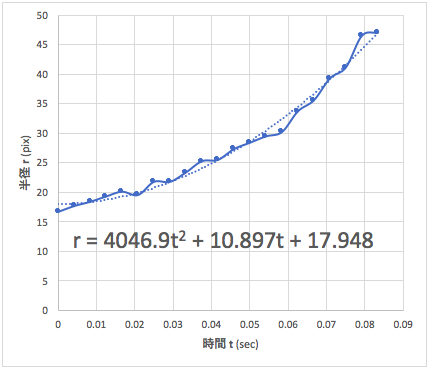
その前に、OpenCVのドキュメントでも記載されているようにハフ変換で検出される r は精度が低くばらつきがあるため、時間 (t) に対する r を最小二乗近似により平滑化します。
測定例をグラフ化してみるとばらつきがわかりますね。

iOS(Swift)で最小二乗（多項式）近似式を求める実装は下記のようになります。
LAPACK の Objective-C 実装である Accelerate.framework を使いました。非モダンな関数に時代を感じますね。。

/// N次の最小二乗近似のパラメータを計算する
/// y = b[0] * x^N + b[1] * x^(N-1) + b[2] * x^(N-2) + ・・・ となるb[] を求める
/// 
/// - Parameters:
///     - points: (x, y)の配列
///     - order: 次数(N) 
/// - Returns: 近似式パラメータの配列
static func leastSquares(points: Array<Array<Float>>, order: Int) -> Array<Double> {
        
    var trans: Int8 = Int8("N".utf8.first!)
    var m: __CLPK_integer = __CLPK_integer(points.count)
    var n: __CLPK_integer = __CLPK_integer(order + 1)
    var b = Array<__CLPK_doublereal>()
    var a = Array<__CLPK_doublereal>()
    for i in (0...order).reversed() {
        for circle in points {
            a.append(__CLPK_doublereal(pow(circle[0], Float(i))))  // x^order の値
            if (i == 0) {
                b.append(__CLPK_doublereal(circle[1]))        // y の値（1列分だけ）
            }   
        }   
    }   
    var work: Array<__CLPK_doublereal> = Array(repeating: 0.0, count: points.count * 2)
    var lda: __CLPK_integer = m 
    var ldb: __CLPK_integer = m 
    var info: __CLPK_integer = 0 
    var ldw: __CLPK_integer = m + n 
    var nrhs: __CLPK_integer=1
        
    dgels_(&trans, &m, &n, &nrhs, &a, &lda, &b, &ldb, &work, &ldw, &info)
        
    return b
}

また、xy 座標ピクセルの距離換算にも、実際のボールの半径との比を使って算出します。
実装（Swift）はこのような感じです。

static let frameTimeDiff: Float = 1.0 / 240.0 // フレーム間の秒
static let depthCalcParamA: Float = 44.874 // 奥行き距離変換の近似式パラメータ（乗数部）
static let depthCalcParamB: Float = -1.015 // 奥行き距離変換の近似式パラメータ（指数部）
static let ballRadius: Float = 0.035 // ボールの半径(m)

/// 円の座標、半径の配列から速度を計算する
/// 
/// - Parameters:
///     - circles: 検出された円(frameIndex, x, y, r)の配列
///     - frameSize: キャプチャ画像のフレームサイズ
/// - Returns: frameIndexごとの速度の配列
static func calcSpeed(circles: Array<Array<Float>>, frameSize: CGSize) -> Array<Array<Float>> {
    // 3次の近似式を出すため、4点以上が必要
    if (circles.count < 4) {
        return []
    }   
        
    // rを2次の最小二乗近似で平滑化する
    var r = Array<Array<Float>>()
    for circle in circles {
        r.append([circle[0] * frameTimeDiff, circle[3]])
    }   
    let rls = leastSquares(points: r, order: 2)
        
    // dx, dy, dzの近似式のパラメータを求める
    var dx = Array<Array<Float>>()
    var dy = Array<Array<Float>>()
    var dz = Array<Array<Float>>()
    for circle in circles {
        let t = circle[0] * frameTimeDiff
        let R = (Float(rls[0]) * t * t + Float(rls[1]) * t + Float(rls[2]))
        dx.append([t, (Float(frameSize.width/2) - circle[1]) * Float(ballRadius) / R]) 
        dy.append([t, (Float(frameSize.height/2) - circle[2]) * Float(ballRadius) / R]) 
        dz.append([t, depthCalcParamA * pow(R, depthCalcParamB)])
    }   
    let xls = leastSquares(points: dx, order: 3)
    let yls = leastSquares(points: dy, order: 3)
    let zls = leastSquares(points: dz, order: 3)

    // ↓ 「4. 3次元実空間におけるボール位置の変化量から速度を算出」へ続く

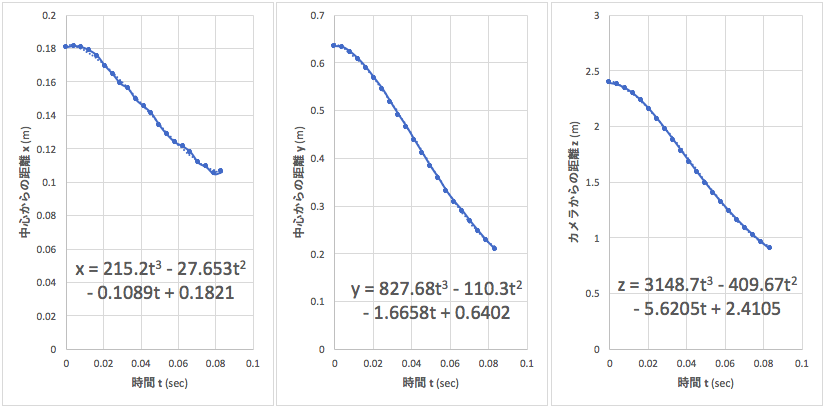
測定例をグラフ化すると、時間(t) に対する空間座標(x, y, z) の値および近似式はこのような感じです。

4. 3次元実空間におけるボール位置の変化量から速度を算出

時間(t) に対する空間座標(x, y, z) の式ができたので、あとはそれぞれ微分して合成速度を求めるだけです。

    // ↑ 「3. 画像における球体の2次元座標を3次元実空間に変換」の続き

    // 微分式から速度を算出
    var speeds = Array<Array<Float>>()
    for circle in circles {
        let t = circle[0] * frameTimeDiff
        let dxdt = (Float(xls[0]) * 3 * t * t) + (Float(xls[1]) * 2 * t) + Float(xls[2])
        let dydt = (Float(yls[0]) * 3 * t * t) + (Float(yls[1]) * 2 * t) + Float(yls[2])
        let dzdt = (Float(zls[0]) * 3 * t * t) + (Float(zls[1]) * 2 * t) + Float(zls[2])
        speeds.append([circle[0], sqrtf(dxdt * dxdt + dydt * dydt + dzdt * dzdt) * 3600 / 1000])
    }   
        
    return speeds
}

5. 結果を表示

各フレームごとに算出した速度は一定ではないので、最終的に何を結果とするかはもはや決めの問題です。
何度か試したところ、検出できた速度列の両端（またはどちらか一方）は極端な数値になることが多かったため、中間60%帯の平均速度を取るのが良さそうです。

自宅で子供が投げたボールを測定した例

こちらは失敗例。。

まとめ

先に結論言っちゃってるのであれなんですが、、実用にはまだまだ工夫が必要ですね。
今回の実験の収穫としては

カメラについてちょっと詳しくなった
ハフ変換はパラメータ次第でそこそこの精度で円を検出できる

というところでしょうか。

それでは、また。

次世代システム研究室では、アプリケーション開発や設計を行うアーキテクトを募集しています。アプリケーション開発者の方、次世代システム研究室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ募集職種一覧からご応募をお願いします。

グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。

Follow @GMO_RD

iPhoneカメラ＆画像認識で球速計測（いわゆるスピードガン）が実現できるか？

結論

考案した仕組み

1. 投球をスローモーション撮影

2. 画像認識で球体検出

どの円を測定対象のボールとみなすか？

3. 画像における球体の2次元座標を3次元実空間に変換

4. 3次元実空間におけるボール位置の変化量から速度を算出

5. 結果を表示

まとめ

関連記事

イマイチ使えなかったスピードガンアプリを実用的にするたったひとつのアイディア

iPhoneXS Max, XR でreact-navigation のヘッダが崩れる問題の解決方法

線画のトレースを題材にしたAR機能の検証

最新の記事

採用情報

インターンシップ

インタビュー

iPhoneカメラ＆画像認識で球速計測（いわゆるスピードガン）が実現できるか？

結論

考案した仕組み

1. 投球をスローモーション撮影

2. 画像認識で球体検出

どの円を測定対象のボールとみなすか？

3. 画像における球体の2次元座標を3次元実空間に変換

4. 3次元実空間におけるボール位置の変化量から速度を算出

5. 結果を表示

まとめ

関連記事

イマイチ使えなかったスピードガンアプリを実用的にするたったひとつのアイディア

iPhoneXS Max, XR でreact-navigation のヘッダが崩れる問題の解決方法

線画のトレースを題材にしたAR機能の検証

タグ

最新の記事

採用情報

インターンシップ

インタビュー