LLM学習の新常識「Muonオプティマイザ」の話

こんにちは、グループ研究開発本部・AI研究開発室のA.Zです

深層学習のオプティマイザというと、一般的によく使われているのはAdam・AdamWです。 この数年間で、Adamオプティマイザはまさに不動の王者として、深層学習におけるデファクトスタンダードとなっています。 しかし、LLMの時代である現在、Adamを超える、より効率的で、よりLLMの特徴に特化したオプティマイザが求められています。 新たに登場したMuon (Momentum Orthogonalization by Newton-Schulz) は、メモリ効率がより良く、かつ学習性能を向上させています。本記事では、Muonの特徴について紹介します。

TL;DR

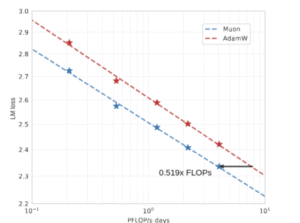
• Muonは従来のAdamオプティマイザと比較して、約半分のメモリを節約でき、大規模言語モデル（LLM）時代において、限られたGPUリソースの中で非常に有利です。
• Muonは学習パラメータ全体をベクターではなく行列として考慮しているため、パラメータ間の関連性や稀なデータの傾向も考慮し、性能と学習能力がより向上します。
• Muonにより、勾配の更新がより正しい方向に行われるため、学習の安定性が向上します。

1. Adamオプティマイザの欠点

Adamは現在最も広く使われているオプティマイザですが、いくつかの重要な欠点があります。特に大規模言語モデル（LLM）の学習において、これらの欠点がより顕著になります。

主な欠点として以下が挙げられます：

• メモリ効率の問題: 一次モメンタムと二次モメンタムの両方を保持する必要があるため、パラメータ数の2倍のメモリが追加で必要
• 行列構造の無視: パラメータを1次元ベクトルとして扱うため、行列としての構造情報が失われる
• 勾配方向の偏り: 頻出パターンに偏った更新が行われ、稀なデータの学習が困難になる

Adamの欠点の詳細話を入り前に、まずAdamというオプティマイザの流れを簡単に紹介します。

• パラメータの勾配計算:
  • パラメータに対する損失関数の勾配を計算
  • $$g_t = \nabla_\theta J(\theta_t)$$
• 一次モメンタムモメンタム値の更新:
  • 一次モメンタムとは各パラメータの勾配の移動平均
  • $$m_t = \beta_1 m_{t-1} + (1 – \beta_1) g_t$$
•  二次モメンタム値の更新:
  • 二次モメンタムとは各パラメータの勾配の二乗の指数移動平均
  • $$v_t = \beta_2 v_{t-1} + (1 – \beta_2) g_t^2$$
•  モメンタムの補正
  • $$\hat{m}_t = \frac{m_t}{(1-\beta_1^t)}$$
  • $$\hat{v}_t = \frac{v_t}{(1-\beta_2^t)}$$
•  パラメータ更新:
  • パラメータ (\(\theta\)) の更新は以下の式で行う

定義：

• \(\theta\): モデルパラメータ
• \(\eta\): 学習率　（ハイパーパラメータ）
• \(g_t\): ｔステップの勾配
• \(m_t\): 一次モメンタム
• \(v_t\): 二次モメンタム
• \(\beta_1, \beta_2\): 移動平均の減衰率（ハイパーパラメータ）
• \(\epsilon\): 0の割り算の回避するための小さい数値

上記のAdamの流れを踏まえて、Adamの欠点を以下に詳しく説明します。

1.1 要素ごとの適応と行列構造の乖離

深層学習でよく利用される線形層は、\(Z = WX\) という行列計算で表現されます。
ここで、\(X\) は入力ベクトル、\(W \in \mathbb{R}^{d_{out} \times d_{in}}\) は学習対象のパラメータ行列です。

しかし、Adamはこの \(W\) をフラットなベクトル（1次元ベクトル）\(\theta \in \mathbb{R}^{N}\)（\(N = d_{out} \times d_{in}\)）とみなし、各要素 \(j\) に対して独立に更新を行います。
Adamの更新則（簡略化したもの）は以下の通りです：

$$\theta_{t+1, j} = \theta_{t, j} – \eta \frac{m_{t, j}}{\sqrt{v_{t, j}} + \epsilon}$$

ここで、\(m_t\) は勾配の一次モーメント、\(v_t\) は二次モーメント（勾配の二乗の移動平均）です。
この式が示しているのは、各パラメータが「他のパラメータとの相関を無視して」、自身の勾配履歴である \(m_t\) と \(v_t\) に基づいてスケーリングされるということです。

 

1.2 モメンタム行列のLow-Rank問題：偏った方向にしか勾配が更新されない

行列 \(W\) の学習において、本来重要なのは行列としての特異値（Singular Values）や固有方向です。
しかし、ベクトルベースのオプティマイザで学習を進めると、モメンタム行列 \(M\)（勾配の移動平均を行列形式に戻したもの）が実用上、低ランクに近い状態に陥りやすいという現象が指摘されています。
これは、勾配情報が特定の少数方向、つまり「更新頻度が高く、勾配が大きい方向」に集中してしまうことを意味します。
その結果、更新量は小さいものの、データの詳細なニュアンスを捉えるために不可欠な方向が埋もれてしまいます。
特にLLMでは、稀なニュアンスや表現、知識などが非常に重要であり、これらの情報が失われると、LLMの性能に大きな影響を与えます。

1.3 一次モメンタムと二次モメンタムによるメモリ使用量の増加

各パラメータに対して、一次モメンタムと二次モメンタムの履歴を保存する必要があるため、メモリ使用量が増加します。
また、1.2 の問題と関連して、偏った方向にしか勾配が更新されないため、それ以外のパラメータに関するモメンタムはほとんど無駄なメモリ領域となり、メモリ効率が悪化します。

 

2. Muonの解決策：モメンタムの直交化 (Orthogonalization)

Muon（MomentUm Orthogonalized by Newton-Schulz）は、2024年10月にKeller Jordan氏（OpenAIエンジニア）によって発表され、急速に注目を集めています。ニューラルネットワークの行列パラメータを対象とし、Newton-Schulz反復法を用いて勾配更新を直交化する手法です。元の紹介ページは以下をご参照ください。

https://kellerjordan.github.io/posts/muon/

Muonのアプローチは、パラメータ更新において「行列の直交性」を強制することです。これにより、支配的な方向だけでなく、すべての基底方向に対して効率的に学習を進めることができます。

2.1 目標：最近傍直交行列の探索

Muonの核心的なアイデアは、現在のモメンタム行列 \(M\) に対して、それに最も近い直交行列 \(O\) を見つけることです。直交行列とは、\(O^T O = I\)（単位行列）を満たす行列であり、ベクトルの長さを保持しながら回転のみを行う性質を持ちます。

この「最近傍直交行列」を求める理由は、勾配更新においてすべての方向を等しく扱うためです。通常のモメンタム行列は特定の方向（大きな勾配を持つ方向）に偏りがちですが、直交化によりすべての基底方向に対して均等な更新を実現できます。

現在のモメンタム行列を \(M\) としたとき、Muonは \(M\) に最も近い直交行列 \(O\) を求め、それを更新に使用します。
数学的には、\(M\) の特異値分解（Singular Value Decomposition, SVD）を用いて以下のように定式化できます。

$$M = U S V^T$$

ここで、\(U\) と \(V\) は直交行列（\(U^T U = I\), \(V^T V = I\)）、\(S\) は特異値 \(\sigma_i\) を対角成分に持つ行列です。

直交化とは、このスケーリング成分 \(S\) を単位行列 \(I\) に置き換える操作に相当します。つまり、元の行列の「方向性」は保持しながら、「大きさ」の情報を正規化することです。

$$O = U I V^T = U V^T$$

この \(O = UV^T\) が直交行列になる理由を確認してみましょう：

$$O^T O = (UV^T)^T (UV^T) = VU^T UV^T = V(U^T U)V^T = VIV^T = VV^T = I$$

ここで、\(U^T U = I\)（\(U\) は直交行列）および \(VV^T = I\)（\(V\) は直交行列）という性質を利用しています。
したがって、\(O^T O = I\) が成り立ち、\(O\) は確実に直交行列となります。

この操作の意味を具体的に説明すると：

• 元のモメンタム行列\(M\) は、異なる方向に対して異なる強度（特異値）を持っています
• 直交化により、すべての方向の強度を1に正規化し、方向性のみを保持します
• これにより、支配的な勾配方向だけでなく、弱い勾配方向も等しく重要視されるようになります
• 結果として、学習がより均衡の取れた方向に進み、局所最適解に陥りにくくなります

これにより、勾配の大きさ（特異値の大小）に依存せず、すべての方向に対して均質な更新ステップを適用することが可能になります。特にLLMの学習では、データの多様性が非常に高く、頻出する話題・単語・表現がある一方で、まれにしか出現しない表現や単語も存在します。弱い勾配も考慮することで、結果的に、まれな表現・単語に関連する能力も維持することができます。

Newton-Schulz反復法による高速化

SVD（特異値分解）は計算量が \(O(N^3)\)と非常に高く、深層学習の各ステップで実行するには現実的ではありません。

そこでMuonは、Newton-Schulz反復法という手法を採用し、計算量の問題を解決します。 Newton-Schulz反復法は、行列の逆数や平方根、そして直交化を効率的に計算するための手法です。この手法は、複雑な行列演算を単純な行列の乗算と加算の組み合わせに変換することで、GPU上での並列計算を可能にします。

基本的に、Newton-Schulz法は以下の式で表されます。

$$
\begin{align*}
X_{k+1} = \Phi(X_k) = a X_k + b X_k X_k^T X_k + \dots & & (1)
\end{align*}
$$

では、上記の式を用いて、Muonが実際にどのようにモメンタム行列（M）の直交行列を計算するのかの流れを説明します。

$$
\begin{align*}
\Phi(M_k) &= a M_k + b M_k M_k^T M_k + c M_k (M_k^T M_k)^2 \\
\Phi(M_k) &= M_k(a I + b M_k M_k^T+c (M_k^T M_k)^2 ) \quad \text{I は単位行列} \\
\end{align*}
$$

モメンタム行列（M）をSVDの形式（\(M=USV^T\)）で置き換えると、展開した式は以下のようになります。

$$
\begin{align*}
\Phi(M_k) &= (U_kS_kV_k^T)(a I + b (U_kS_kV_k^T) (U_kS_kV_k^T)^T + c (U_kS_kV_k^T) (U_kS_kV_k^T)^T (U_kS_kV_k^T) (U_kS_kV_k^T)^T ) \\
\Phi(M_k) &= (U_kS_kV_k^T)_k(a I + b (U_kS_kV_k^TV_kS_kU_k^T)+c (U_kS_kV_k^TV_kS_kU_k^T) (U_kS_kV_k^TV_kS_kU_k^T)) \\
\end{align*}
$$

\(VV^T=I\) および \(UU^T=I\) の性質を利用すると、さらに以下のように整理できます。

$$
\begin{align*}
\Phi(M_k) &= (U_kS_kV_k^T)_k(a I + b (U_k S_k S_k U_k^T) + c (U_k S_k S_k U_k^T) (U_k S_k S_k U_k^T))\\
\Phi(M_k) &= (U_kS_kV_k^T)_k(a I + b (U_k S_k^2 U_k^T) + c (U_k S_k^2 S_k^2 U_k^T))\\
\Phi(M_k) &= (U_kS_kV_k^T)_k(a I + b (U_k S_k^2 U_k^T) + c (U_k S_k^4 U_k^T))\\
\Phi(M_k) &= (U_kS_kV_k^T)_k(a I + b (U_k S_k^2 U_k^T) + c (U_k S_k^4 U_k^T))\\
\Phi(M_k) &= (aU_kS_kV_k^T)+ (b U_k S_k^2 U_k^T U_k S_k V_k) + (c U_k S_k^4 U_k^T U_k S_k V_k)\\
\Phi(M_k) &= (aU_kS_kV_k^T)+ (b U_k S_k^3 V_k) + (c U_k S_k^5 V_k)\\
\Phi(M_k) &= U_k(aS_k+bS_k^3+cS_k^5)V_k^T & & (2)\\
\end{align*}
$$

上記の結果から、\(a\)、\(b\)、\(c\) というパラメータは以下の多項式に適用されます。

$$\varphi(x) = ax + bx^3 + cx^5$$

この調整の最終目標は以下のとおりです：

• すべての特異値（範囲は0.0〜1.0）が、最小限のイテレーション回数で1.0に収束するようにします。
  • すべての特異値が1.0に収束すると、数式(2)より、\(S_k\)​が単位行列となり、残るのは直交行列\(U_kV_k^T\) のみとなります。

適切な \(a\)、\(b\)、\(c\) のパラメータを設定し、数式(1)に適用することで、行列の掛け算・足し算のみで直交行列を近似的に計算することができます。

Muonでは、\(a\)、\(b\)、\(c\) のパラメータが事前に最適化されており、最も適切な値は以下のとおりです。

a, b, c = (3.4445, -4.7750,  2.0315)

こちらの手法の実装はPytorchで、以下で実装されます。

def zeropower_via_newtonschulz5(G, steps: int):
    """
    Newton-Schulz iteration to compute the zeroth power / orthogonalization of G. We opt to use a
    quintic iteration whose coefficients are selected to maximize the slope at zero. For the purpose
    of minimizing steps, it turns out to be empirically effective to keep increasing the slope at
    zero even beyond the point where the iteration no longer converges all the way to one everywhere
    on the interval. This iteration therefore does not produce UV^T but rather something like US'V^T
    where S' is diagonal with S_{ii}' ~ Uniform(0.5, 1.5), which turns out not to hurt model
    performance at all relative to UV^T, where USV^T = G is the SVD.
    """
    assert G.ndim >= 2 # batched Muon implementation by @scottjmaddox, and put into practice in the record by @YouJiacheng
    a, b, c = (3.4445, -4.7750,  2.0315)
    X = G.bfloat16()
    if G.size(-2) > G.size(-1):
        X = X.mT

    # Ensure spectral norm is at most 1
    X = X / (X.norm(dim=(-2, -1), keepdim=True) + 1e-7)
    # Perform the NS iterations
    for _ in range(steps):
        A = X @ X.mT
        B = b * A + c * A @ A # quintic computation strategy adapted from suggestion by @jxbz, @leloykun, and @YouJiacheng
        X = a * X + B @ X
    
    if G.size(-2) > G.size(-1):
        X = X.mT
    return X

Newton-Schulzの手法を利用することで、GPUが効率的に実行できる行列掛け算・足し算のみで、高速で直交行列の計算することができます。

2.2 第一次モメンタムのみを利用し、メモリー削減

最終的に、Muonのアルゴリズムは以下のとおりです。

上記から、必要なのは一次モメンタムのみで、Adamが利用した二次モメンタムがなくなっています。その結果、必要なメモリー量が理論上、約半分に削減することができます。 毎回のパラメーター更新で、直交行列の計算のオーバーヘッドが発生しますが、アルゴリズム的にGPUが効率的に実行することができるため、大規模モデル学習にはGPUメモリーコストに比べて、許容されると思います。 直交行列を用いることで、学習率がより改善されるという結果が発表されたので、精度の上でもMuonほうがAdamよりも優れていると言えます。

3. Muonの事例または成果

Moonshot AI社のKIMI 2 LLMに応用

現在公開されている事例の中で、最も注目されるのはMoonshot AI社のKIMI2 LLMの学習への応用事例です。

https://arxiv.org/pdf/2502.16982

KIMI 2は最近のLLMモデルの中で性能的に上位グループに位置するモデルであり、学習にはMuonベースの独自手法を使用していました。

LLM学習において、Adamと比較した主な効果は以下の通りです。

• 学習の計算リソース効率が約2倍向上
  •   
• 学習スピードは約20%向上
  • 
• 学習の安定性の向上
  • LLMの学習でよく発生する勾配やLossのスパイクを回避
  • 
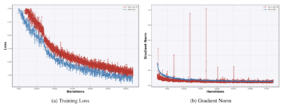
  • ※ Muonでの学習は青、Adamでの学習は赤

それ以外の事例

以下のページでは、いくつかのポジティブな結果が報告されます。

https://github.com/KellerJordan/Muon?tab=readme-ov-file#accomplishments

 

まとめ

今回は、Muonという新たな機械学習のオプティマイザについて紹介しました。現在最も一般的に利用されている手法であるAdamと比較して、計算リソース効率、学習効率、安定性の向上という結果が報告されています。 特に大規模言語モデル（LLM）の学習では、もともと膨大なリソースや時間が必要とされるため、Muonの効果がより発揮されると考えられます。

PyTorch版のMuonのライブラリが以下に公開されました。ぜひ機会があれば、お試しください。

https://github.com/KellerJordan/Muon

最後に

グループ研究開発本部 AI研究開発室では、データサイエンティスト/機械学習エンジニアを募集しています。ビッグデータの解析業務などAI研究開発室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。皆さんのご応募をお待ちしています。

参考：

• https://kellerjordan.github.io/posts/muon/
• https://discuss.huggingface.co/t/tutorial-understanding-and-implementing-the-muon-optimizer/167717
• https://glorious-potato-19.notion.site/Understanding-Muon-A-Revolutionary-Neural-Network-Optimizer-233ffa7f40c4800eafa5cc843e039327