金融時系列データのノイズ除去

はじめに：金融データとノイズの問題

こんにちは。グループ研究開発本部・AI研究開発室のR.I.です。

資産運用やリスク管理の実務において、共分散行列（Covariance Matrix）は非常に重要な役割を果たします。現代ポートフォリオ理論（MPT）に基づく平均分散最適化や、リスクファクター分析（PCA）、CAPMにおけるベータ計算など、多くの数理モデルが「資産間の相関」を入力データとして要求するからです。

しかし、実務家はしばしば「教科書通りの最適化を行うと、極端なウェイト配分になり、将来のパフォーマンスが不安定になる」という問題に直面します。この主な原因の一つが、共分散行列に含まれる「ノイズ」です。

金融データは、資産数（N）に対して観測期間（T）が十分でないケースが多く、推定された相関係数には偶然による見せかけの相関が大量に含まれています。本記事では、Marcos López de Prado氏の著書『Machine Learning for Asset Managers』第2章を参考に、ランダム行列理論（RMT）を用いてこのノイズを除去する手法を解説・実装します。

ランダム行列理論とマルチェンコ・パスツール分布

ノイズを除去するには、まず「何がノイズで、何がシグナル（情報）なのか」を定義する必要があります。ランダム行列理論（RMT）は、完全にランダムなデータから生成された相関行列の固有値分布を記述することで、この基準を与えてくれます。

Marchenko-Pastur定理

平均0、分散 σ^2 の独立同分布（IID）に従うランダム行列 X（サイズ T × N）から作成された相関行列の固有値 λ は、TとNが十分に大きいとき、ある特定の確率密度関数（PDF）に従うことが知られています。

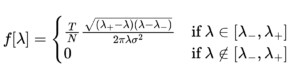
ここで重要になるのが、固有値が取りうる範囲です。理論的な上限（λ+）と下限（λ-）は以下の式で与えられます。

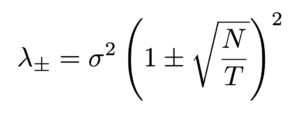
この定理が示唆するのは、「λ+ 以下の固有値はランダムなノイズと区別がつかない」ということです。逆に言えば、λ+ を超える大きな固有値こそが、市場の構造的要因（シグナル）を含んでいると考えられます。

ノイズ除去（Denoising）のアルゴリズム

具体的なノイズ除去の手順は以下の通りです。ここでは「Constant Residual Eigenvalue Method」と呼ばれる手法を採用します。

1. 固有値分解: 相関行列を固有値分解し、固有値と固有ベクトルを取得します。
2. 分布のフィッティング: 固有値のヒストグラムに対し、マルチェンコ・パスツール分布（MP分布）をフィッティングさせ、ノイズの分散 σ^2 を推定します。これにより、理論的な閾値 λ+ が決定されます。
3. 固有値の修正:
   • λ+ より大きい固有値（シグナル）はそのまま維持します。
   • λ+ 以下の固有値（ノイズ）は、それらの平均値で置き換えます。これにより、ノイズ部分の総分散を維持しつつ、ランダムな変動を平滑化します。
4. 再構築: 修正された固有値と元の固有ベクトルを用いて、相関行列を再構築します。

Pythonによる実装と検証

では、実際にPythonで実装してみましょう。ここでは書籍のコードスニペットを参考にしつつ、自分の環境で動作するように実装したコードを使用します。

1. 必要なライブラリとMP分布関数の定義

まず、理論的な確率密度関数（PDF）を定義します。

import numpy as np
import pandas as pd
from scipy.optimize import minimize
from sklearn.neighbors import KernelDensity
import matplotlib.pyplot as plt

# マルチェンコ・パスツール分布の理論PDF
def mp_pdf(var, q, pts):
    e_min = var * (1 - (1./q)**.5)**2
    e_max = var * (1 + (1./q)**.5)**2
    e_val = np.linspace(e_min, e_max, pts)
    pdf = q / (2 * np.pi * var * e_val) * np.sqrt((e_max - e_val) * (e_val - e_min))
    pdf = np.nan_to_num(pdf)
    return pd.Series(pdf, index=e_val)

2. ノイズ除去（Denoising）関数の実装

次に、ノイズと判定された固有値を平均化して行列を再構築する関数を実装します。

# 相関行列からデノイズされた相関行列を生成する関数
def denoised_corr(e_val, e_vec, n_facts):
    # e_val: 固有値（対角行列）, e_vec: 固有ベクトル, n_facts: シグナルとみなす固有値の数
    
    e_val_ = np.diag(e_val).copy()
    # ノイズ部分（n_facts以降）を平均値で置換
    e_val_[n_facts:] = e_val_[n_facts:].sum() / float(e_val_.shape[0] - n_facts)
    
    # 固有値を対角行列に戻す
    e_val_ = np.diag(e_val_)
    
    # 相関行列の再構築
    cov = np.dot(e_vec, e_val_).dot(e_vec.T)
    
    # 対角成分を1にする正規化（相関行列化）
    inv_std = np.diag(1. / np.sqrt(np.diag(cov)))
    corr_denoised = np.dot(inv_std, cov).dot(inv_std)
    
    return corr_denoised

3. 実験：擬似データへの適用

シグナルを含んだランダム行列を生成し、まずはその固有値分布が理論通りになっているかを確認します。ここで、理論分布（MP分布）と実際の固有値分布（ヒストグラム）を重ねてプロットすることで、ノイズの範囲を視覚的に特定します。

# データ生成パラメータ
N, T = 1000, 10000
q = T / N
np.random.seed(42)

# ランダムなリターン行列（ノイズ）を作成
x = np.random.normal(0, 1, size=(T, N))

# 相関行列と固有値計算
corr = np.corrcoef(x, rowvar=0)
e_val, e_vec = np.linalg.eigh(corr)

# 固有値を降順にソート（扱いやすくするため）
idx = e_val.argsort()[::-1]
e_val, e_vec = e_val[idx], e_vec[:, idx]

# 理論的な閾値（分散1と仮定）
e_max = (1 + (1./q)**.5)**2

# --- プロットによる確認 ---
fig, ax = plt.subplots(figsize=(10, 6))

# 1. 実データの固有値分布（ヒストグラム）
ax.hist(e_val, density=True, bins=50, alpha=0.5, label='Empirical PDF')

# 2. 理論的なマルチェンコ・パスツール分布（曲線）
# 理論値の計算（分散=1.0として計算）
pdf_theory = mp_pdf(1., q, 1000)
ax.plot(pdf_theory.index, pdf_theory.values, color='r', linewidth=2, label='Marcenko-Pastur PDF')

ax.set_title('Eigenvalue Distribution: Empirical vs Theoretical')
ax.set_xlabel('Eigenvalue')
ax.set_ylabel('Probability Density')
ax.legend()
plt.grid(True, alpha=0.3)
plt.show()

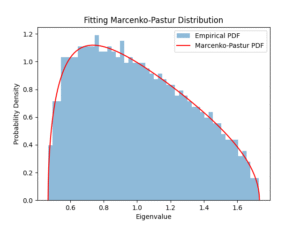
図1で、赤い曲線は「完全にランダムなノイズ」が従うべき分布を示しています。実際の固有値（青いヒストグラム）がこの範囲内に綺麗に収まっている場合、それらはノイズとみなせます。

この赤い曲線の右端が、理論上の最大固有値 λ+ です。実際の金融データでは、この右端よりもさらに右側に「はみ出した」固有値が現れることがあり、それこそが我々が抽出したい「シグナル」だと考えることができます。

次に、この境界線（λ+）を使って、ノイズ部分を除去（Denoising）します。

# シグナル数の判定
# lambda_max (e_max) よりも大きい固有値の個数をカウント
n_facts = e_val.shape[0] - np.searchsorted(e_val[::-1], e_max)

# デノイズ実行
corr_denoised = denoised_corr(e_val, e_vec, n_facts)

print(f"最大理論固有値 (lambda+): {e_max:.4f}")
print(f"検出されたシグナル数: {n_facts}")

print("\n--- デノイズ前の相関行列（一部） ---")
print(corr[:3, :3])

print("\n--- デノイズ後の相関行列（一部） ---")
print(corr_denoised[:3, :3])

実行結果として、以下のような出力が得られました。

最大理論固有値: 1.7325
検出されたシグナル数: 0

--- デノイズ前の相関行列（一部） ---
[[ 1.         -0.01637975 -0.00545305]
[-0.01637975  1.         -0.00426415]
[-0.00545305 -0.00426415  1.        ]]

--- デノイズ後の相関行列（一部） ---
[[ 1.00000000e+00 -2.57744705e-17 -6.06795077e-18]
[-3.60718190e-17  1.00000000e+00 -3.52258734e-16]
[-4.43379780e-18 -3.52697292e-16  1.00000000e+00]]

この手法により、ノイズのみで構成された成分はゼロに近い小さな値へと平準化され、行列全体の安定性が向上します。

実データを用いた実験

擬似データでの動作確認ができたので、次は実データを用いた検証実験を行います。

実験の目的

デノイズされた共分散行列を用いることで、ポートフォリオのアウトオブサンプル（将来）のリスク（分散）を低減できるかを検証します。

データセットと前処理

• 対象資産: S&P 500構成銘柄のうち、欠損なくデータが取得できた75銘柄（生存バイアスがありますが、手法間の相対比較のため許容します）。
• 期間: 2018年1月〜2025年12月。
• 前処理: 日次調整済み終値から対数収益率を計算し、全期間データが存在する銘柄のみを使用しました。

比較対象（ベンチマーク）

1. 標本共分散行列（Sample Covariance）: 何も加工しない通常の行列。
2. Shrinkage法（Ledoit-Wolf）: 従来の統計的手法による正則化。
3. デノイズ共分散行列（本手法）: RMTに基づきノイズ除去した行列。

検証プロセス（Rolling Window法）

時系列データの特性を考慮し、ローリングウィンドウ方式で検証を行いました。

1. 学習期間（In-sample）: 過去252日分（約1年）のデータを用いて、3種類の共分散行列を推定します。
2. ポートフォリオ構築: 各共分散行列を用いて「最小分散ポートフォリオ（Minimum Variance Portfolio）」のウェイトを計算します。
3. 評価（Out-of-sample）: 計算したウェイトを翌日の市場データに適用し、リターンを記録します。
4. スライド: ウィンドウを1日ずらし、上記を繰り返します。

実験結果

約8年間のバックテストを行った結果、各手法のポートフォリオの年率化ボラティリティ（リスク）は以下のようになりました。また、各手法の累積リターンを図2に示します。

• Sample Covariance: 16.4%
• Shrinkage (Ledoit-Wolf): 15.1%
• Denoised (RMT): 15.4%

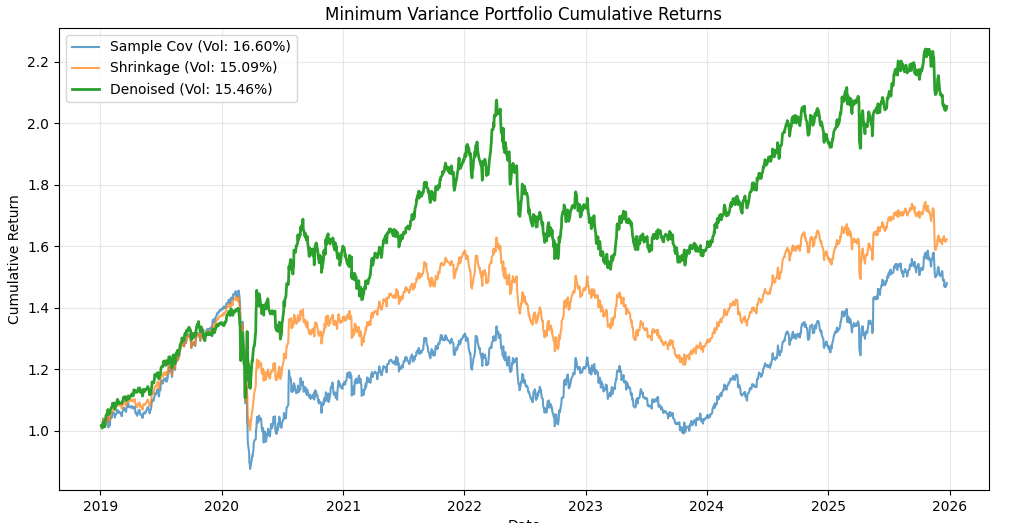
S&P 500構成銘柄（N=75）を用いた実験の結果、Shrinkage法とデノイズ手法（RMT）が、標本共分散行列（Sample Covariance）よりもリスクを低減させることが確認できました。

今回の実験ではShrinkage法が最も優れたパフォーマンスを示しましたが、RMTによるデノイズも標本共分散行列よりは明確に改善しており、有効性が示唆されました。さらに資産数が多い場合（N > Tのケースなど）では、これらの手法の重要性はさらに高まると予想されます。

まとめ

本記事では、金融データの共分散行列に含まれる「ノイズ」の問題と、それをランダム行列理論を用いて除去する手法について解説しました。

• 金融データは N/T 比が大きく、標本共分散行列はノイズの影響を強く受ける。
• マルチェンコ・パスツール分布を用いることで、理論的にノイズとシグナルを分離できる。
• ノイズ部分の固有値を平均化することで、シグナルを維持しつつ行列を安定化できる（Denoising）。

さいごに

グループ研究開発本部 AI研究開発室では、データサイエンティスト/機械学習エンジニアを募集しています。ビッグデータの解析業務などAI研究開発室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ募集職種一覧からご応募をお願いします。皆さんのご応募をお待ちしています。

参考資料